DGLAs and obstruction theory

The purpose of this post, the third in a series on deformation theory and DGLAs, is to describe the obstruction theory for a formal moduli problem associated to a DGLA.

1. Tangent-obstruction theories

Standard problems in classical deformation theory usually have a “tangent-obstruction theory” parametrized by certain successive cohomology groups. For example, let’s consider the problem of deformations of a smooth variety ${X}$ over an algebraically closed field ${k}$ , over finite-dimensional local ${k}$ -algebras. Then:

The “infinitesimal automorphisms” of ${X}$ —that is, automorphisms of the trivial deformation over ${k[\epsilon]/\epsilon^2}$ —are given by ${H^0( X, T_X)}$ where ${T_X}$ is the tangent bundle (i.e., vector fields).
The isomorphism classes of deformations of ${X}$ over the dual numbers ${k[\epsilon]/\epsilon^2}$ are given by ${H^1(X, T_X)}$ .
There is an obstruction theory with ${H^1, H^2}$ . Specifically, given a square-zero extension of finite-dimensional local ${k}$ -algebras
$\displaystyle 0 \rightarrow I \rightarrow A' \rightarrow A \rightarrow 0,$

and given a deformation ${\xi}$ of ${X}$ over ${\mathrm{Spec} A}$ , there is a functorial obstruction in ${H^2(X, T_X) \otimes_k I}$ to extending the deformation over the inclusion ${\mathrm{Spec} A \hookrightarrow \mathrm{Spec} A'}$ .
In the previous item, if the obstruction vanishes, then the isomorphism classes of extensions of ${\xi}$ over ${\mathrm{Spec} A'}$ are a torsor for ${H^1(X, T_X) \otimes_k I}$ .

One has a similar picture for other deformation problems, for example deformations of vector bundles or closed subschemes. The “derived” approach to deformation theory provides (at least in characteristic zero) a general explanation for this phenomenon.

Suppose now ${\mathrm{char} k = 0}$ , and let ${\mathfrak{g}}$ be a DGLA over ${k}$ . Then ${\mathfrak{g}}$ defines a formal moduli problem. In the previous post, we sketched a construction of this. Given a dg-artinian ${k}$ -algebra ${A}$ , we defined:

$\displaystyle \Sigma_{\mathfrak{g}}(A) = MC( \mathfrak{g} \otimes \mathfrak{m}_A),$

for ${\mathfrak{m}_A \subset A}$ the maximal ideal, where ${MC}$ refers to the “space of solutions of the Maurer-Cartan equation.”

The moduli problem ${\Sigma_{\mathfrak{g}}}$ lives in the derived world—it takes values in spaces. But we can get a classical formal moduli problem by sending an ordinary artinian ring ${A}$ to ${\pi_0( \Sigma_{\mathfrak{g}}(A))}$ . Call this functor ${\tau_{\leq 0} \Sigma_{\mathfrak{g}}}$ —it’s the type of functor that would be studied in classical deformation theory. Let’s see how the analysis at the beginning of this post would play out for ${\tau_{\leq 0} \mathfrak{g}}$ .

Example 1 The “tangent space” ${\tau_{\leq 0}( k[\epsilon]/\epsilon^2)}$ is given precisely by ${H_{-1}(\mathfrak{g})}$ . The Maurer-Cartan elements of ${\mathfrak{g} \otimes \mathfrak{m}_A}$ correspond in this case precisely to the cycles in ${\mathfrak{g}_{-1}}$ , and the equivalence relation on them turns out exactly to be cohomology.

In general, given a formal moduli problem, one can associate a “tangent complex” (in ${k}$ -chain complexes) to it—for ${\Sigma_{\mathfrak{g}}}$ , the associated tangent spectrum is ${\mathfrak{g}[-1]}$ . The truncation ${\tau_{\leq 0} \Sigma_{\mathfrak{g}}}$ doesn’t remember all of ${\mathfrak{g}}$ , just ${H_{-1}}$ .

Example 2 If we remembered the automorphisms (but not higher automorphisms) and considered instead the truncation ${\tau_{\leq 1} \mathfrak{g}}$ , then the automorphisms (or ${\pi_1}$ ) would be given by ${H_0( \mathfrak{g})}$ . In general, we’ll see that

$\displaystyle \Sigma_{\mathfrak{g}}(k[\epsilon]/\epsilon^2) = \Omega^\infty \mathfrak{g}[1];$

this’ll be a part of the definition of the tangent spectrum.

Example 3 Let’s now consider the most interesting part—obstruction theories. The claim is that there is an obstruction theory for ${\Sigma_{\mathfrak{g}}}$ with coefficients ${H_{-2}(\mathfrak{g})}$ .

More specifically, consider a square-zero extension

$\displaystyle 0 \rightarrow I \rightarrow A' \rightarrow A \rightarrow 0.$

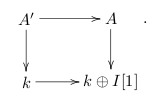
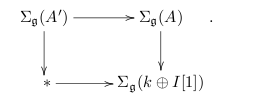
In this case, there is a cartesian square

That’s the derived point-of-view on square-zero extensions—the extension map ${A \rightarrow I[1]}$ is (or rather, acquires the structure of) a derivation, and that leads to a map ${A \rightarrow k \oplus I[1]}$ . (This can be written down explicitly with cdgas.)

By the cohesiveness axiom, this leads to a homotopy cartesian square of spaces,

In particular, given a point in ${\pi_0 ( \Sigma_{\mathfrak{g}}(A))}$ , it can be lifted to ${\Sigma_{\mathfrak{g}}(A')}$ if and only if it maps to the basepoint in in ${\pi_0 \Sigma_{\mathfrak{g}}( k \oplus I[1]) = H_{-2}( \mathfrak{g}) \otimes_k I}$ . (Moreover, the set of lifts is a torsor over ${H_{-1}( \mathfrak{g}) \otimes_k I}$ .)

In this way, it follows that there is always a canonical tangent-obstruction theory derived directly from the DGLA, and the obstruction theory can be interpreted simply in terms of the long exact sequence of a fibration. The naturality of the obstruction theory (which can be observed classically, without DGLAs) has many useful applications.

Example 4: In the problem of lifting a deformation from $\mathrm{Spec} k[\epsilon]/\epsilon^2$ to $\mathrm{Spec} k[\epsilon]/\epsilon^3$ , we note that the first object is represented by a cycle $x$ in $\mathfrak{g}_{-1}$ —or rather $\epsilon x$ . The Maurer-Cartan equation states simply that it is a cycle. But to lift it to a Maurer-Cartan element modulo $\epsilon^2$ , the obstruction becomes precisely $[x, x]$ .

2. Hilb and Pic

(I learned this from Mumford’s Lectures on curves on an algebraic surface.)

Let ${X}$ be a smooth, projective surface over the algebraically closed field of characteristic zero. A natural object of study is the collection of curves on ${X}$ . This set is not simply a set; it acquires the structure of a scheme. In other words, there is a scheme ${\mathrm{Curves}_X}$ which parametrizes curves (or rather, flat families of curves) on ${X}$ . The scheme ${\mathrm{Curves}_X}$ is a disjoint union of components of the Hilbert scheme ${\mathrm{Hilb}_X}$ .

Let’s say we are trying to construct families of curves on ${X}$ . Given a curve ${C \subset X}$ , the tangent space to ${\mathrm{Curves}_X}$ at ${C}$ is given by

$\displaystyle H^0( C, \mathcal{N}_{X/C}),$

as one would expect: a field of normal vectors should give an infinitesimal way to wiggle ${C}$ . One can prove this (i.e., compute the tangent space to ${\mathrm{Curves}_X}$ ) by using the moduli interpretation, and by studying flat families of curves over ${\mathrm{Spec} k[\epsilon]/\epsilon^2}$ .

More generally, the DGLA for the deformation problem “imbedded deformations of ${C}$ in ${X}$ ” is given by (derived) global sections of the sheaf of DGLAs which is the homotopy fiber of the map

$\displaystyle T_C \rightarrow (T_X)|_C,$

that is, the normal sheaf shifted by ${-1}$ : ${\mathcal{N}_C[-1]}$ .

In other words, we expect to construct a ${h^0( C, \mathcal{N}_{X/C})}$ -dimensional family of deformations of ${C}$ . However, we can’t necessarily do this, because ${\mathrm{Curves}_X}$ is not necessarily smooth at ${C}$ . What we’ve just done is compute the embedding dimension (dimension of the Zariski tangent space), while we want the Krull dimension. To do this, we’ll need to study higher order deformations and obstructions, and for this we’ll need a bit more about the global geometry of ${\mathrm{Curves}_X}$ .

3. The map to the Picard scheme

Let’s keep the notation of the previous section. There are many curves on ${X}$ , but there is also an equivalence relation one can impose on them: linear equivalence. Curves may move in ${\mathbb{P}^1}$ -families, and we can break the problem of studying curves on ${X}$ into two pieces: studying the various ${\mathbb{P}^1}$ families and studying the equivalence classes. Let’s see this in the following example of a criterion for smoothness of ${\mathrm{Curves}_X}$ .

In more sophisticated terms, one has a morphism

$\displaystyle p: \mathrm{Curves}_X \rightarrow \mathrm{Pic}_X ,$

sending a curve ${C \subset X}$ to the line bundle ${\mathcal{O}_X(C)}$ . In order to understand ${\mathrm{Curves}_X}$ , one wants to understand the base and the fibers.

The fiber of ${p}$ over a line bundle ${\mathcal{L} \in \mathrm{Pic}_X}$ consists of all curves in the linear equivalence class ${\mathcal{L}}$ : that is, the projective space ${\mathbb{P}( H^0(\mathcal{L})^{\vee}) }$ . So, understanding the fibers of ${p}$ is a question of computing some dimensions, which we can try to get at via Riemann-Roch type formulas.
The target ${\mathrm{Pic}_X}$ is a proper group scheme, and since the characteristic is zero, it is smooth (hence an abelian variety).

If ${C}$ is a smooth curve, then the normal bundle on ${C}$ is given by ${\mathcal{O}(C)/\mathcal{O}}$ , so that we have an exact sequence

$\displaystyle 0 \rightarrow \mathcal{O}_X \rightarrow \mathcal{O}_X(C) \rightarrow \mathcal{N}_C \rightarrow 0.$

Theorem (Severi-Kodaira-Spencer) Let ${C}$ be a curve such that the map ${H^1( \mathcal{O}_X(C)) \rightarrow H^1( C, \mathcal{N}_C)}$ is zero. Then ${\mathrm{Curves}_X}$ is smooth at ${C}$ .

Proof sketch: There is a canonical obstruction theory for deformations of ${C}$ in ${X}$ , given by ${H^1(\mathcal{N}_C)}$ . Similarly, there is a canonical obstruction theory for deformations of line bundles on ${X}$ , given by ${H^2( X, \mathcal{O}_X)}$ . The DGLA associated to this problem is given by ${\mathbf{R}\Gamma( \mathcal{O}_X)/k}$ .

The map of deformation problems ${\mathrm{Curves}_X \rightarrow \mathrm{Pic}_X}$ induces (say via DGLA theory) a map of obstruction theories that one can identify as coming from the coboundary map

$\displaystyle H^1( C, \mathcal{N}_C)) \rightarrow H^2( X, \mathcal{O}_X).$

By hypothesis, this map is injective.

Therefore, to show that the obstructions to deforming ${C}$ in ${\mathrm{Curves}_X}$ vanish, it suffices to show that the obstructions vanish in ${H^2(X, \mathcal{O}_X)}$ . But the obstructions there vanish because ${\mathrm{Pic}_X}$ is smooth and there are no obstructions to deforming a line bundle. $\Box$

Climbing Mount Bourbaki