Intersection theory on surfaces II

Let ${S}$ be a smooth, projective surface over an algebraically closed field ${k}$ and let ${C, D \subset S}$ be curves (subschemes pure of codimension one) on ${S}$ . In the previous post, we discussed what a good theory of intersections ${C.D}$ would look like. We wanted to be able to define the intersection ${C.D}$ in such a manner that:

If ${C, D}$ intersect transversely, then ${C.D = |C \cap D|}$ .
The intersection product is additive. That is, given curves ${C_1, C_2, D}$ , we have
$\displaystyle (C_1 + C_2). D = C_1.D + C_2.D,$

where ${C_1+C_2}$ is treated as an effective Cartier divisor.
The intersection product is invariant under linear equivalence and descends to a pairing on the Picard group.

1. Definition of the intersection product

In the previous post, we saw that any intersection theory as above was necessarily unique, and suggested that the Euler characteristic formula

$\displaystyle C.D \stackrel{\mathrm{def}}{=} \chi( \mathcal{O}_C \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D ) = \sum_i (-1)^i \mathbb{H}^i( \mathcal{O}_C \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D) \ \ \ \ \ (1)$

would be a good definition: i.e., that the failure of

$\displaystyle C.D = |C \cap D|$

in general was due to two factors: the existence of nilpotents in the (scheme-theoretic as opposed to set-theoretic) intersection ${C \cap D}$ and higher homotopy groups in the (derived as opposed to scheme-theoretic) intersection ${C \stackrel{h}{\cap} D}$ . The main goal of this post is to prove that (1)does give a good theory. That is, we would like to prove:

Theorem 1 The definition of ${C.D}$ in (1) satisfies the conditions desired of an intersection product.

Proof: This is now relatively “formal” to prove, except for additivity. If ${C, D}$ intersect transversely, then

$\displaystyle \mathcal{O}_C \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D \simeq \mathcal{O}_C \otimes_{\mathcal{O}_S} \mathcal{O}_D;$

that is, there are no higher homotopy groups in the “derived” intersection. Moreover, the intersection is only a finite collection of reduced points, so the above Euler characteristic formula counts them. To prove this, observe that if ${p \in C \cap D}$ , then there exist ${f,g \in \mathcal{O}_{S, p}}$ such that ${f}$ cuts out ${C}$ , ${g}$ cuts out ${D}$ (scheme-theoretically), and ${(f,g) = \mathfrak{m}_{S, p}}$ . This means

$\displaystyle ( \mathcal{O}_{S,p}/(f)) \stackrel{\mathbb{L}}{ \otimes}_{\mathcal{O}_{S, p}} ( \mathcal{O}_{S,p}/(g)) \simeq k,$

because ${f,g}$ form a regular sequence. This shows that the “derived” intersection is the ordinary set-theoretic one and proves the first claim.

Now let’s check that the intersection ${C.D}$ depends only on the linear equivalence class of ${C}$ (and by the evident symmetry in the definition, in ${D}$ ). We have an exact sequence

$\displaystyle 0 \rightarrow \mathcal{O}_{S}(-C) \rightarrow \mathcal{O}_{S} \rightarrow \mathcal{O}_C \rightarrow 0,$

which gives an exact triangle (in the derived category)

$\displaystyle \mathcal{O}_{S}(-C) \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D \rightarrow \mathcal{O}_{S} \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D\rightarrow \mathcal{O}_C \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D\rightarrow.$

In particular, we find that

$\displaystyle C.D = \chi( \mathcal{O}_{S} \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D ) - \chi( \mathcal{O}_{S}(-C) \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D). \ \ \ \ \ (2)$

This clearly only depends on the line bundle associated to ${C}$ . This proves that the intersection pairing depends only on the linear equivalence class. $\Box$

2. Proof of additivity

The additivity of the intersection product is the “non-formal” part of the above proof, and it relies on the fact that we are working with surfaces. Let’s first obtain another formula for the intersection number. We saw in the previous section that

$\displaystyle C.D = \chi( \mathcal{O}_{S} \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D ) - \chi( \mathcal{O}_{S}(-C) \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S} \mathcal{O}_D) ,$

and, using the exact sequence

$\displaystyle 0 \rightarrow \mathcal{O}_S(-D) \rightarrow \mathcal{O}_S \rightarrow \mathcal{O}_D \rightarrow 0,$

we conclude the following useful formula:

$\displaystyle C.D = \chi(\mathcal{O}_S) - \chi(\mathcal{O}_S(-C)) - \chi(\mathcal{O}_S(-D)) + \chi( \mathcal{O}_S(-C - D)). \ \ \ \ \ (3)$

Let ${A}$ be an abelian group. We say that a function

$\displaystyle f: A \rightarrow \mathbb{Z}$

is polynomial of degree ${\leq p}$ if, for any map ${\mathbb{Z}^n \rightarrow A}$ , the composite

$\displaystyle \mathbb{Z}^n \rightarrow A \stackrel{f}{\rightarrow} \mathbb{Z}$

is given by a polynomial of (total) degree ${\leq p}$ in its arguments. If ${f}$ is quadratic (i.e., polynomial of degree ${\leq 2}$ ), then the difference

$\displaystyle x, y \mapsto f(x+y) - f(x) - f(y) + f(0),$

defines a symmetric bilinear form on ${A}$ . In order to prove additivity of the intersection numbers, it thus suffices to prove that the Euler characteristic is a quadratic function on the Picard group of a surface. More generally:

Theorem 2 (Snapper) Let ${X}$ be a projective variety of dimension ${n}$ . Then the Euler characteristic

$\displaystyle \chi: \mathrm{Pic}(X) \rightarrow \mathbb{Z}$

is polynomial of degree ${\leq n}$ .

Proof: The proof is induction on ${\dim X}$ . Without loss of generality, assume ${X}$ irreducible.

Let ${\mathbb{Z}^m \rightarrow \mathrm{Pic}(X)}$ be a homomorphism. By possibly expanding ${m}$ , we can assume that a very ample line bundle ${\mathcal{L}}$ is in the image. By an appropriate change of basis of ${\mathbb{Z}^m}$ , we may also assume that each of the coordinate vectors ${e_i = (0, 0, \dots, 0, 1, 0, \dots, 0)}$ maps to a very ample line bundle on ${X}$ .

Now if ${\mathcal{L}}$ is very ample, we have a global nonzero section ${s \in \Gamma(X, \mathcal{L})}$ whose zero locus ${X_H \subset X}$ is of dimension ${\leq n-1}$ . The exact sequence

$\displaystyle 0 \rightarrow \mathcal{L}^{-1} \rightarrow \mathcal{O}_{X_H} \rightarrow \mathcal{O}_{X_H} \rightarrow 0$

shows that

$\displaystyle f(x - \mathcal{L}) - f(x)$

is a polynomial function of degree ${\leq n-1}$ , by induction on the dimension. In particular, for each ${i}$ , we find that ${f(x-e_i) - f(x)}$ is a polynomial function on ${\mathrm{Pic}(X)}$ of degree ${\leq n-1}$ . The next lemma now shows that ${f}$ is a polynomial function of degree ${\leq n}$ . $\Box$

Lemma 3 Let ${f: \mathbb{Z}^m \rightarrow \mathbb{Z}}$ be a function. Suppose for each basis element ${e_i}$ , ${x \mapsto f(x+e_i) - f(x)}$ is polynomial of degree ${\leq n-1}$ . Then ${f}$ is polynomial of degree ${\leq n}$ .

Proof: First, observe that the assertion is straightforward when ${m=1}$ . We will use this case below.

The hypothesis implies that ${f(x + y) - f(x)}$ is polynomial of degree ${\leq n-1}$ for any ${y \in \mathbb{Z}^m}$ . By induction on ${m}$ , we may assume that ${f|_{\mathbb{Z}^{m-1}}}$ is polynomial of degree ${\leq n}$ . Then

$\displaystyle f(x_1, \dots, x_m) = f(x_1, \dots, x_{m-1}, 0) + \sum_{i=0}^{x_m-1} \left(f(x_1, \dots, x_{m-1}, i+1) - f(x_1, \dots, x_{m-1}, i)\right)$

is polynomial of degree ${\leq n+1}$ . Since the restriction of ${f}$ to any line has degree ${\leq n}$ , we are done. $\Box$

Over the complex numbers, Snapper’s theorem has a simple proof via Hirzebruch-Riemann-Roch, which states that for any vector bundle ${\mathcal{V}}$ on a complex manifold ${M}$ , the holomorphic Euler characteristic can be computed topologically:

$\displaystyle \chi(\mathcal{V}) = \int_{M} \mathrm{Todd}(T_M) \mathrm{ch}(V) .\ \ \ \ \ (4)$

The Chern character of a line bundle ${\mathcal{L}}$ is ${e^{ c_1(\mathcal{L})}}$ , which varies polynomially in ${\mathcal{L}}$ since ${c_1}$ is additive in ${\mathcal{L}}$ and since we are working on a finite-dimensional space. Thus the integral that computes ${\chi(\mathcal{L})}$ is polynomial in ${\mathcal{L}}$ , and the polynomial is of degree at most the (complex) dimension.

3. Examples

Let’s now try to make this a bit more concrete. Let ${C, D \subset S}$ be curves. Suppose ${C, D}$ have no common irreducible component. This implies that the derived tensor product ${\mathcal{O}_C \stackrel{\mathbb{L}}{\otimes}_{\mathcal{O}_S}\mathcal{O}_D}$ is the ordinary tensor product. In fact, near a point ${p \in C \cap D}$ , ${C}$ is cut out by an equation ${f}$ and ${D}$ is cut out by an equation ${g}$ . Since

$\displaystyle \mathcal{O}_{S, p}/(f,g)$

is an artinian local ring, it follows that ${(f,g)}$ must be a regular sequence. In this case, we have

$\displaystyle C.D = \dim_k \Gamma(C \cap D, \mathcal{O}_{C\cap D}), \ \ \ \ \ (5)$

where we do not need derived tensor products to make the intersection, but we do need nilpotents (and schemes).

Let’s now make a calculation that works even to calculate the self-intersection of a curve. We have ${C.D = \chi( \mathcal{O}_C \stackrel{\mathbb{L}}{\otimes} \mathcal{O}_D)}$ , and as we saw that implied (see (2))

$\displaystyle C.D = \chi( \mathcal{O}_D) - \chi(\mathcal{O}_D(-C)).$

If ${D}$ is smooth, this is equivalently the degree of the line bundle ${\mathcal{O}(C)}$ on ${D}$ : in fact, this is a consequence of the Riemann-Roch theorem for curves. So we conclude:

Proposition 4 If ${D}$ is a smooth curve, then ${C.D = \mathrm{deg}( \mathcal{O}_D(C))}$ .

In particular, if ${C \subset S}$ is a smooth curve, then the self-intersection ${C.C }$ can be calculated as the degree of ${\mathcal{O}(C)|_C}$ . The adjunction formula gives that

$\displaystyle \mathcal{O}(C)|_C = N_{C/S}$

is the normal bundle of ${C}$ in ${S}$ , so we find that the self-intersection of a curve in ${S}$ is the degree of its normal bundle.

hilbertthm90 Says:

January 28, 2013 at 1:00 pm

There’s something weird about saying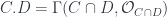 $C.D=\Gamma (C\cap D, \mathcal{O}_{C\cap D})$ . Should the word length be in there (I always confuse these terms, maybe not length, but something like it)?

Akhil Mathew Says:

January 28, 2013 at 3:56 pm
Yes, in fact I should have said the length (or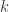 $k$ -dimension). That was a typo which I’ve now fixed; thanks for pointing it out.

Climbing Mount Bourbaki