Segal’s approach to delooping

(This is the second post devoted to unpacking some of the ideas in Segal’s paper “Categories and cohomology theories.” The first is here.)

Earlier, I described an observation (due to Beck) that loop spaces could be characterized as algebras over the monad ${\Omega \Sigma}$ . At least, any loop space was necessarily an algebra over that monad, and conversely any algebra over that monad was homotopy equivalent to a loop space. There is an alternative and compelling idea of Segal which gives a condition somewhat easier to check.

As far as I understand, most of the different approaches to delooping a space consist of imitating the classical construction for a topological group ${G}$ : the construction of the space ${BG}$ . It is known that any topological group ${G}$ is (weakly) homotopy equivalent ${\Omega BG}$ , and conversely (though perhaps it is not as well known) that any loop space is homotopy equivalent to a topological group. (This can be proved using the simplicial construction of Kan.) Given a space (which may not be a topological group), the idea is that delooping machinery will assume given just enough structure to build something analogous to the classifying space, and then build that. This is, for instance, how the construction of Beck ran.

Here’s Segal’s idea; it is quite similar to the ${\Gamma}$ -idea. Given a topological group ${G}$ , we can construct ${BG}$ using a standard simplicial construction. If ${G}$ is only a group object in the homotopy category, we can’t run this construction. Segal decides just to assume that one has given the data of a simplicial object that behaves like ${BG }$ should and runs with that.

The starting point is that one can encode the structure of a monoid in a simplicial set. Given a monoid ${G}$ , the simplicial set ${BG}$ has the following properties.

${(BG)_0}$ is a point.
The map ${(BG)_n \rightarrow \prod_{i=1}^n (BG)_1}$ induced by the ${n}$ inclusions ${[1] \rightarrow [n]}$ (sending ${0}$ and ${1}$ to consecutive elements) is an isomorphism.

In fact, if we have any simplicial set with the above properties, it determines a unique monoid. This is proved in a similar way. If ${X_\bullet}$ is such a simplicial set, then we take ${X_1}$ as the underlying set of the monoid, and the map ${X_1 \times X_1 \rightarrow X}$ comes from the boundary map ${X_2 \rightarrow X_1}$ ; the identity element comes from the map ${X_0 = \ast \rightarrow X_1}$ . So monoids can be described as simplicial sets satisfying certain properties (just as commutative monoids can).

As before, we can weaken this by replacing “isomorphism” by “homotopy equivalence.”

Definition 4 An S-datum is a simplicial space (e.g. bisimplicial set) ${X_\bullet}$ with the following properties.

${X_0}$ is (weakly) contractible.

The map ${(X)_n \rightarrow \prod_{i=1}^n (X)_1}$ induced by the ${n}$ inclusions ${[1] \rightarrow [n]}$ (sending ${0}$ and ${1}$ to consecutive elements) is a weak equivalence.

The terminology should not be taken seriously because I just made it up.

As before, an S-datum determines an honest monoid object in the homotopy category, given by ${X_1}$ . The S-datum consists of a lifting of the associated simplicial object in the homotopy category to the category of topological spaces, and we will see that it allows one to build a classifying space. As we will see, a connected space which is not a loop space cannot admit an S-datum in this way. An incidental consequence is the existence of diagrams in the homotopy category of spaces which cannot be lifted to the category of spaces (choose a connected, homotopy associative H space which is not a loop space); see this MO question for simpler examples.

1. Segal’s result

The next result is the analog of the fact that ${G \simeq \Omega BG}$ .

Theorem 5 (Segal) If ${X_\bullet}$ is an S-datum and ${X_1}$ is connected, then we have a weak equivalence

$\displaystyle X_1 \simeq \Omega |X_\bullet|.$

The proof of this relies on a bit of homotopy theory, of the formal and categorical flavor. The strategy is to work simplicially throughout, so ${X_\bullet}$ is really a bisimplicial set—that is, a simplicial object in the category of simplicial sets. Then the “geometric realization” ${|X_\bullet|}$ (which is itself a simplicial set) can be thought of in two ways: first of all, it is the “diagonal” simplicial set. If we think of ${X}$ as a family of sets ${X_{n,m}}$ depending on two parameters ${n, m}$ (because of the double occurrence of the word “simplicial”), then the diagonal simplicial set is ${d(X)_n := X_{n, n}}$ . For another approach, it is the “homotopy colimit” (or higher categorical colimit) of the individual simplicial sets ${X_n}$ .

Now, the statement of Segal’s theorem is that there should be a homotopy cartesian diagram

where ${\ast}$ is really a stand-in for a contractible space. We will construct ${\ast}$ by taking the “simplicial path space.” Namely, we consider the map functor ${\phi}$ which sends ${[n] \rightarrow [n+1]}$ , and to a simplicial object ${T_\bullet}$ we take ${T_{\bullet \circ \phi}}$ . There is an “extra degeneracy,” which means that the simplicial path space is always contractible, and its geometric realization must be too.

So, we’ve started with this simplicial space (space meaning “simplicial set”) ${X_\bullet}$ , and we’ve formed the contractible simplicial space ${PX_\bullet}$ ; this has the property that

$\displaystyle PX_n = X_{n+1}.$

Thus we get a morphism of simplicial spaces ${PX_\bullet \rightarrow X_\bullet}$ (which is given by the last face map), such that the geometric realization of ${PX_\bullet}$ is (weakly) contractible. There is a commutative diagram

This comes from the natural imbedding of the zero-simplices in the geometric realization, at each stage. If we can prove that (1) is homotopy cartesian, then we’ll be done.

Now we are in the following situation. We have an indexing category ${\mathcal{I} }$ , and two functors ${F, G: \mathcal{I} \rightarrow \mathbf{SSet}}$ . There is a natural tranformation ${F \rightarrow G}$ , which induces a natural transformation

$\displaystyle {\mathrm{hocolim} F \to \mathrm{hocolim}G.}$

Here ${\mathrm{hocolim}}$ can be given explicitly using the Bousfield-Kan formula. Then we have ${i \in I}$ , and we want to show that the induced diagram

is homotopy cartesian.

2. A technical result

This distributivity property desired is certainly not true in general. However, there is a result that gives a criterion for this to happen.

Theorem 6 Consider two functors ${F, G: \mathcal{I} \rightarrow \mathbf{SSet}}$ with the property that for each morphism ${i \rightarrow j}$ in ${\mathcal{I}}$ , there is a homotopy cartesian diagram

Then there are homotopy cartesian diagrams for each ${i}$ as in (2).

Let’s take this result as a black box (a nice reference is this paper of Charles Rezk), and use it to prove the theorem of Segal. We have a morphism of simplicial spaces (bisimplicial sets) ${PX_\bullet \rightarrow X_\bullet}$ , and we have to check the homotopy cartesian criterion of the above theorem to show that ${X_1 \simeq \Omega |X_\bullet|}$ as claimed.

So, what we need to do is to show that for any map ${j: n \rightarrow m}$ , the diagram

is homotopy cartesian.

Here is an example of what is going on. Let’s take ${n = 0}$ , so we have the diagram

where the first horizontal map is, up to homotopy, the iterated multiplication ${(X_1)^{m+1} \rightarrow X_1}$ and the first vertical map is, up to homotopy, multiplication of two of the factors ${(X_1)^{m+1} \rightarrow (X_1)^m}$ . We have to check that the homotopy fibers are the same. The homotopy fiber on the right is clearly ${X_1}$ . On the other hand, we have:

Lemma 7 Let ${X}$ be a connected H space. Then the homotopy fiber of the multiplication ${\mu: X \times X \rightarrow X}$ is just ${X}$ itself, imbedded via ${x \mapsto (x, i(x))}$ for ${i}$ a homotopy inverse.

Proof: In fact, we can assume that ${X}$ is a CW complex, in which case ${X}$ is automatically an H-group, or a group object in the homotopy category. To see this, one has to show that ${X}$ is a group object in the homotopy category, which amounts to saying that the “shearing” map

$\displaystyle X \times X \rightarrow X \times X, \quad (x,y) \mapsto (\mu(xy), y)$

is a homotopy equivalence. For this, we need to check that it is an isomorphism on homotopy groups by Whitehead’s theorem. It is an isomorphism on ${\pi_0}$ by hypothesis, and on the higher homotopy groups it corresponds to the shearing map on homotopy groups (by the Eckmann-Hilton argument). These shearing maps are clearly isomorphisms, so ${X}$ must be an H group.

Anyway, we can consider the sequence

$\displaystyle X \stackrel{(1, i)}{\rightarrow} X \times X \stackrel{\mu}{\rightarrow} X$

which we claim is a fiber sequence. However, since the composite is nullhomotopic, we get a map from ${X}$ to the homotopy fiber of ${\mu}$ . If we check on homotopy groups, we can see directly that it is a homotopy equivalence. $\Box$

Anyway, what all this amounts to is that the requisite diagrams all turn out to be homotopy cartesian. And then we can apply Theorem 6 above to conclude that (1) is homotopy cartesian, which finishes the proof.

3. Comments

Maybe it’s worth saying something about “Theorem 6” above, the bit of categorical machinery used in this proof. In some sense, it is saying that homotopy colimits distribute over (homotopy) fiber products. The analogy with the word “homotopy” removed is one of the distinguishing characteristics of a Grothendieck topos. Homotopy limits and colimits should be thought of as higher categorical versions of ordinary limits and colimits, so perhaps what Theorem 6 is expressing is none other than the fact that the $(\infty, 1)$ -category of spaces (the analog of the ordinary category of sets) is an $(\infty, 1)$ -topos.

But I don’t actually know anything about higher topos theory, and Peter May provided on MO some reasons why I probably shouldn’t try too hard to change that in the near future. So elaborating on the previous paragraph (or acquiring the knowledge to be able to do so) will probably take me some time!

Alex Says:

March 10, 2012 at 6:51 am

Hi! Can you explain more precisely the fact about equivalence of loop space and topological group? Does or not this equivalence respect h-group structure? (here i mean h-commutativity of obvious square with morphisms and multiplications). I know very little about such things, but the case of natural equivalence G=\Omega BG seemed to respect h-group law – for U(n) this equivalence can be seen from holonomy of unitary connection on tautological bundle given by projection from outer space of grassmanian G(n,\infty).
Sorry for my bad english

Akhil Mathew Says:

March 10, 2012 at 11:23 pm
Hi Alex,

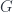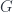Given a topological group $G$ , one has a fiber sequence $G \to EG \to BG$ , which exhibits $G$ as the loop space of 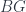$BG$ , with the correct H structure. One way to see this is from the explicit simplicial construction of 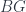$BG$ : for each element of 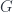$G$ , you get a 1-simplex (that’s the loop on 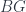$BG$ ), and whenever you have elements $g_1, g_2$ , you have a 2-simplex connecting the composite of the 1-simplices for $g_1, g_2$ and the one for $g_1g_2$ . 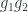This latter condition means precisely that $G \to \Omega BG$ is a morphism of H spaces.

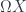As for the equivalence: one way of saying it is that any path fibration $\Omega X \to PX \to X$ (up to homotopy) arises from a topological group (namely, a topological group modelling $\Omega X$ ). Expressed simplicially, you can even get a Quillen equivalence between simplicial groups and connected simplicial sets: one the one hand, you have the “loop group” and on the other you have the classifying space. (This is explained in Goerss-Jardine.)