The etale fundamental group of an algebraic group is not necessarily abelian

As of late, I’ve been reading the proof due to Laumon of the Weil conjectures (a simplification of Deligne’s second proof) via the Fourier-Deligne transform. This is quite interesting, and I’d like to start a series of posts on it soon, based on the notes I’ve been taking. I don’t currently have the time to edit the notes, so I’ll devote this post to a curious fact I learned today.

One of the first results one proves when studying the classical fundamental group in topology is that the fundamental group of a topological group is abelian. As I learned today, the analogous result for the etale fundamental group fails.

Let $G_0$ be a smooth group scheme, defined over a finite field $\kappa$ of size $q$ , and let $G$ be the base-change to the algebraic closure. Then there is the Lang map $L: G \to G$ sending $x \mapsto (Fx) x^{-1}$ , for $F$ the Frobenius.

It is a theorem (of Lang) that this map $L$ is a surjective map. It is also finite, since the fiber over the identity is finite (the $\kappa$ -rational points), and a morphism of homogeneous spaces for an algebraic group with finite fibers is finite. (Quick but probably unnecessarily non-elementary proof: a morphism of reduced homogeneous spaces over a smooth group scheme is faithfully flat, by generic flatness and a translation argument. As a result, it’s a quotient map. Since the fibers are finite, one can check that the map is closed by a similar translation argument. Then, proper plus finite fibers implies finite by Zariski’s Main Theorem.)

Also, the Frobenius induces the zero map on the tangent spaces. As a result, $x \mapsto (Fx) x^{-1}$ , the Lang morphism, is smooth as the morphism on tangent spaces is a bijection. So, since the fibers are finite, we have an etale cover!

The claim is that it is a Galois cover, and the automorphism group is $G_0(\kappa)$ : indeed, the right translations by the $\kappa$ -rational points are automorphisms of the cover. Since this is the right number of translations for the degree of the cover, we have indeed a Galois cover with the appropriate Galois group. But, in general, this Galois group won’t be abelian. So the fundamental group, which surjects onto every Galois group, can’t be abelian either.

I initially tried to prove the false result by the Eckmann-Hilton argument (until I was told about this counterexample), but it seems not to be correct: perhaps the problem is that the etale fundamental group doesn’t commute with products! (It does for proper schemes over an algebraically closed field, but this is very nontrivial.)

hilbertthm90 Says:

July 23, 2011 at 10:17 pm

Until your last sentence I was going to ask if you thought it was a fault of positive characteristic or of non-algebraically closedness that caused this, but it seems that algebraically closed may be the bigger problem?

Akhil Mathew Says:

July 24, 2011 at 7:33 am
The example I gave was for an algebraically closed field! The nonzero characteristic seems to be the problem (see my response to Qiaochu’s comment).

1. hilbertthm90 Says:
  
  July 24, 2011 at 1:43 pm
  Oops. When I thought back about it I forgot that we had base changed to the algebraic closure. I just remembered the finite field part.

Qiaochu Yuan Says:

July 23, 2011 at 11:48 pm

Well, my naive guess is that etale covers in positive characteristic can be weird, so I’m not completely surprised by this. Is the result true in characteristic zero?

Akhil Mathew Says:

July 24, 2011 at 7:32 am
I’m pretty sure abelianness holds in characteristic zero. We can reduce to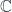 $\mathbb{C}$ as base field (by the “Lefschetz principle”), and then the Riemann existence theorem states that the etale fundamental group is the profinite completion of the fundamental group of the analytification, and the latter is a topological group, so it’ll be abelian.

1. Akhil Mathew Says:
  
  July 24, 2011 at 7:43 am
  Er, actually we need to be sure that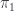 $\pi_1$ is unaffected by extensions of an algebraically closed field. This is true for a proper scheme, but probably not for a non-proper scheme in characteristic $p$ . Let me think… (It’s true for abelianizations by base-change results on \’etale cohomology.)

Johan Says:

July 24, 2011 at 7:06 am

Any finite p-group can occur as the Galois group of a finite etale covering of the affine line over an algebraically closed field k of characteristic p.

Yes, the fundamental group does not commute with products of varieties over k. For example if S = Spec(A) is an affine scheme of characteristic p, then H^1(S, Z/pZ) is the cokernel of the map A —> A which maps a to a^p – a. Now consider A = k[x, y] = k[x] \otimes_k k[y]. Then xy gives an element in H^1 which is not a sum of elements of H^1(Spec(k[x]) and H^1(Spec(k[y]).

Akhil Mathew Says:

July 24, 2011 at 7:46 am
Thanks. The example Gaitsgory showed me was the same as yours, but the reasoning was that any local system on $A^2$ would then be a tensor product of ones over each factor, but this is not true, by the example of the Artin-Schreier sheaf pulled back by multiplication map.

Do you know if this is true in characteristic zero? The only obstacle I can see is whether the fundamental group commutes with base-change of an algebraically closed field, which I remember was true for proper schemes. But in char. 0 it seems it ought to work.

1. Jason Starr Says:
  
  July 26, 2011 at 9:41 am
  What about central étale isogenies of semisimple groups? There must be some correct interpretation of “simply connected” semisimple groups in positive characteristic.
  
2. Johan Says:
  
  July 27, 2011 at 1:06 pm
  In char zero you can compare the \pi_1 with the topological \pi_1 (because change of alg closed base field is OK in char 0) and then you can use the result for topological spaces. I think you probably already figured this out though.
  
  1. Akhil Mathew Says:
    
    July 27, 2011 at 11:22 pm
    Ah. This is the step I was missing: I thought the change of algebraically closed base field was only true in the proper case, as in SGA 1. Thanks for clearing that up.
    
    1. Johan Says:
      
      July 28, 2011 at 10:02 am
      Yeah, hmm, if X is a smooth variety over an algebraically closed field of char 0, then choose an open immersion X —> Y into a smooth proper variety Y such that the complement is a divisor with normal crossings. (This uses resolution of singularities, but you can avoid it.) Now in char 0 you can see that any finite etale covering of X has a “predictable” behaviour along the boundary (Abhyankar’s lemma). In particular, the coverings you get do not have “moduli”. This is the key step in proving invariance under algebraically closed field extensions, although when you look at the proof the thing about moduli won’t show up directly.
      
      The same argument works for the _tame_ fundamental group in char p (although you don’t have resolutions of singularities, so you first reduce to the case of a curve or a surface by some tricks).
      
      1. Akhil Mathew Says:
        
        July 28, 2011 at 9:21 pm
        Hmm. I guess the result is pretty nontrivial then! I couldn’t recall it from SGA1.

Tenth Linkfest Says:

August 21, 2012 at 1:08 pm

[…] Akhil Mathew: The etale fundamental group of an algebraic group is not necessarily abelian […]

Climbing Mount Bourbaki