Earlier, our proof of the vanishing of higher quasi-coherent cohomology on an affine was actually very incomplete. We actually computed only Cech cohomology, and waved our hands while pointing to a fancy sheaf-theoretic result of Cartan. I would like to prove this result today, following Godement’s Theorie des faisceaux.
Cech cohomology is (comparatively) easy to compute, for instance via the Koszul complex. But the problem is that we don’t a priori know if coincides with derived functor cohomology. We have a natural map between Cech and derived functor cohomology in any case, but in general it won’t be an isomorphism. Leray’s theorem is a sufficient condition for this, but its expression is fundamentally in terms of derived functor cohomology: you have to have an acyclic covering–a covering on which the derived functor cohomology is trivial. But a priori, how can we tell that an open set is acyclic? What if we only know Cech cohomology? The point of today’s post is to use the heavy machinery of the Cech-to-derived functor spectral sequence to get such a purely Cech-theoretical criterion.
Cartan’s theorem gives a sufficient criterion for this to be the case. The result is:
Theorem 42 Let
be a space,
a sheaf on
. Suppose there is a basis
of open sets on
, closed under finite intersections, satisfying the following condition. If
is a finite open covering of
, then the Cech cohomology in positive dimension vanishes,
Then the natural map:
is an isomorphism, for any
I confess to having stated the result earlier incorrectly, when I claimed that the conclusion was for
.
But in any case, this will finally(!) complete the proof of the vanishing of the higher quasi-coherent cohomology of an affine. For then we just take to be the collection of basic open affines. We have shown that the Cech cohomology with respect to this family covers vanishes (on the whole space and on any basic open set, which is also affine!).
The proof is an inductive argument and a reduction to the theorem of Leray. Namely, we are going to show that the (derived functor) cohomology of on any element in this basis
vanishes. This means that the theorem of Leray goes into effect and gives us the conclusion, since you can always compute derived functor cohomology by Cech cohomology on an acyclic covering. Consider the following statement, which I’ll call
. For any
, and
,
is trivial. If we prove all the
, then we will see that
is an acyclic cover of
, and we can use it to compute sheaf cohomology for
.
Suppose is true. So
is identically zero on the basis
. Fix
. Then in the spectral sequence for Cech-to-derived-functor cohomology, things degenerate at
, and we find that
(Here denotes Cech cohomology of
over the open set
—this can be computed using sets in the basis
.)
More precisely, on and below the diagonal of the
page, everything in the spectral sequence is zero except on the horizontal row. This is because
is zero on open sets in
and the spectral sequence looks like
Anyway, from the boxed equation, we find from the hypotheses about that
. Since
was arbitrary, this proves
. We can now climb up the natural numbers and see that the Leray theorem applies. [Edit: As pointed out below in the comments, there’s an extra step here to show that the Cech
of the presheaves
vanish, which follows from the fact that any class in the (derived functor) cohomology of a sheaf is always locally trivial.]
This completes the proof. And, finally, since we have spent an obscene amount of time on this, we can use to our heart’s content that quasi-coherent cohomology is trivial on an affine, even if you’re working with non-noetherian schemes!
There is now the question of where to go next. I would like to spend a little time on basic algebro-geometric results about cohomology. In particular, I want to compute the cohomology of line bundles on projective space, since that will be an application of the preceding result as well as another Koszul complex argument. I don’t want to spend too much time on that though—the big highlights of Zariski’s main theorem and the formal function theorem will come only much later, after I’ve discussed the foundational proper mapping theorem—since the theme for November is Koszul-type stuff. So instead, I plan to talk about local cohomology.
November 19, 2010 at 3:58 pm
For the past week I’ve been obsessing over some of the tedious details of Cech cohomology vs sheaf cohomology. There are (somewhat mild) conditions you can put on schemes to get the two to agree, but I was wondering if there were known mild conditions you could put on stacks to guarantee that they agree.
This spectral sequence type of thing gives conditions, but they are not very helpful in trying to frame them as conditions on the stacks, and there doesn’t seem to be anything written down anywhere about it.
The only thing I keep running into is that if you use Cech hypercovers rather than covers, then they will always agree (this is from SGA 4 expose V).
November 19, 2010 at 4:21 pm
Unfortunately I don’t really know any good criteria other than Leray’s theorem, and e.g. its application to separated schemes (and I know nothing about Artin stacks at this point).
June 14, 2013 at 12:04 pm
I think I’m missing something obvious here – but how does the zeroth Cech cohomology group vanish when you do induction?
June 14, 2013 at 10:31 pm
It doesn’t — the inductive hypothesis only deals with the positive-dimensional cohomology groups.
June 15, 2013 at 1:30 am
In that case, why is there no $H^0(\mathfrak{A},U,\mathcal{H}^k(\mathcal{F}))$ in the boxed equation? In Grothendieck spectral sequence in the previous post, does the index $p$ start from 1 rather than 0?
June 21, 2013 at 10:06 pm
Sorry for the slow response.
The inductive assumption is that $H^i(U, \mathcal{F}) = 0$ for $U$ an open subset in the cover and $1 \leq i < k$ (I seem to have written $1 < i$, but for $i = 1$ Cech cohomology is the same as derived functor cohomology). Moreover, one has the assumption that the Cech cohomology of $\mathcal{F}$ on $U$ vanishes.
Together, the two claims above imply that every term in the spectral sequence on the relevant diagonal is already zero at $E_2$.
If I've understood correctly, the answer to your question is that the second claim (which is part of the hypothesis of the theorem).
June 23, 2013 at 1:16 pm
Sorry, but I seem to be still missing something. If I understood your notations correctly, the $H^0$ term I mentioned is the zeroth Cech cohomology of the presheaf $U \to H^k(U,F)$, where $H^k$ is the derived functor cohomology rather than Cech, so I can’t see how the Cech assumption on $\mathcal{F}$ can be used. The spectral sequence would however imply that the presheaf just mentioned is actually a sheaf. Does that have any consequence?
June 23, 2013 at 11:27 pm
Ah, I see your point. Yes, that should have been in the post. The reason is that the Cech of the *presheaf*
of the *presheaf* 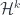 is always zero for
is always zero for  : that is, any cohomology class (in derived functor cohomology) of a sheaf is always locally trivial.
: that is, any cohomology class (in derived functor cohomology) of a sheaf is always locally trivial.
To prove this, it suffices to show that the sheafification of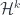 is zero. Sheafification is exact, so the sheafification of
is zero. Sheafification is exact, so the sheafification of 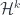 is the
is the 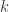 th derived functor of the sheafification of
th derived functor of the sheafification of  , which is the identity.
, which is the identity.
Thanks for catching that.
July 2, 2013 at 12:34 am
Thanks! That clarifies the issue.