It is possible to define sheaves on a Grothendieck topology. Before doing so, let us recall the definition of a sheaf of sets on a topological space {X}.

Definition 1 A sheaf of sets {\mathcal{F}} assigns to each open set {U \subset X} a set {\mathcal{F}(U)} (called the set of sections over {U}) together with “restriction” maps {\mathrm{res}^U_V: \mathcal{F}(U) \rightarrow \mathcal{F}(V)} for inclusions {V \subset U} such that the following conditions are satisfied:

  • {\mathrm{res}^U_U = \mathrm{id}} and for a tower {W \subset V \subset U}, the composite {\mathrm{res}^V_W \circ \mathrm{res}^U_V } equals {\mathrm{res}^U_W}.
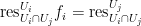
  • If {\left\{U_i\right\}} is a cover of {U \subset X}, then the map \displaystyle \mathcal{F}(U) \rightarrow \prod \mathcal{F}(U_i) is injective, and the image consists of those families {f_i \in \mathcal{F}(U_i)} such that the restrictions to the intersections are equal \displaystyle \mathrm{res}^{U_i}_{U_i \cap U_j} f_i = \mathrm{res}^{U_j}_{U_i \cap U_j}

    In particular, this says that if we have a family of elements {f_i \in \mathcal{F}(U_i)} that satisfy the above gluing condition, then there is a unique {f \in \mathcal{F}(U)} which restricts to each of them.


An equivalent, and more elegant, way of stating the gluing condition is that

\displaystyle \mathcal{F}(U) \rightarrow \prod_I \mathcal{F}(U_i) \rightrightarrows \prod \mathcal{F}(U_i \cap U_j)

is an equalizer diagram of sets.

This definition was intended to be a review. The main point is that the only “topological notions” we actually used were:

  1. The intersections {U_i \cap U_j}
  2. The statement that {\left\{U_i\right\}} covered {U}.

However, we can express both categorically if we have a site {\mathfrak{C}}; the intersections are given by fibered products, and the covering is given by the Grothendieck topology.

Definition 2 Let {\mathfrak{C}} be a site. A sheaf of sets on {\mathfrak{C}} is a contravariant functor {\mathcal{F}: \mathfrak{C} \rightarrow \mathbf{Sets}} such that if {\left\{U_i \rightarrow U\right\}} is a covering, then the sequence\displaystyle \mathcal{F}(U) \rightarrow \prod_I \mathcal{F}(U_i) \rightrightarrows \prod \mathcal{F}(U_i \cap U_j)

is an equalizer diagram of sets.

The interpretation of the restriction maps as a contravariant functor makes the definition simpler. Note that a sheaf of sets on the category of open sets of a topological space {X} with the usual Grothendieck topology is the same thing as a sheaf of sets on the topological space itself; this is obvious from the definitions.

It is of course possible to define sheaves of abelian groups, rings, etc. on a site. The only extra condition is that, for a morphism {X \rightarrow Y} in the category, the “restriction” maps {\mathcal{F}(Y) \rightarrow \mathcal{F}(X)} are required to be homomorphisms of the requisite algebraic structure.

Recall that in standard algebraic geometry, we inevitably encounter presheaves. A presheaf is kind of like a sheaf in that there are restriction maps, but we do not require that sections can be glued. Similarly, we can define this on a site:

Definition 3 A presheaf of sets on a site {\mathfrak{C}} is a contravariant functor {\mathfrak{C} \rightarrow \mathbf{Sets}}.

Clearly, it is possible to define a morphism of presheaves (or sheaves) in a manner generalizing the usual one.

Definition 4 A morphism of presheaves (or sheaves) {\mathcal{F} \rightarrow \mathcal{G}} is defined as a natural transformation of functors. In other words, there are maps {\mathcal{F}(U) \rightarrow \mathcal{G}(U)} for each {U} in the site, and these commute with the restriction maps. There is thus a category of presheaves (resp. sheaves) on {\mathfrak{C}}, which we write as {\mathbf{PreSh}(\mathfrak{C})} (resp. {\mathbf{Sh}(\mathfrak{C})}). Since a sheaf is just a special type of presheaf, there is a fully faithful functor {\mathbf{PreSh}(\mathfrak{C}) \rightarrow \mathbf{Sh}(\mathfrak{C})}.

It is well-known that given a presheaf on a topological space, it is possible to functorially associate a “sheafification,” such that homming out of the sheafification into a sheaf is the same thing as homming out of the initial presheaf. In other words, the forgetful functor from presheaves to sheaves has an adjoint. This is also true over a site; I will not prove it, since I am not planning to go too much into the categorical side of things here.

We will show that representable functors (which are contravariant functors to the category of sets, hence presheaves) are actually sheaves in many interesting cases over schemes.

Proposition 5 Let {\mathfrak{C}} be the category of {S}-schemes with the Zariski topology (i.e. a covering is a collection of open immersions with jointly surjective image). Let {F: \mathfrak{C} \rightarrow \mathbf{Sets}} be a representable (contravariant) functor. Then {F} is a sheaf in the Zariski topology.

Proof: This result turns out to be trivial! Indeed, let {\left\{U_i \rightarrow U\right\}} be a covering. We can assume that each {U_i} is an open subset of {U}. Then the claim is that the sequence

\displaystyle \mathcal{F}(U) \rightarrow \prod_I \mathcal{F}(U_i) \rightrightarrows \prod \mathcal{F}(U_i \cap U_j)

is exact.

Now {F} is, up to natural isomorphism (which doesn’t affect anything) {\hom_S(-, Z)} for {Z} a suitable {S}-scheme. Exactness at the first level says that if we have two morphisms {U \rightarrow Z} such the restrictions to {U_i} are the same, then two morphisms are the same; this is clear, since two morphisms that are the same locally are the same everywhere. The second level says that if we have morphisms {U_i \rightarrow Z} that glue on {U_i \cap U_j}, then we can define {U \rightarrow Z}. This is clear; given {x \in U}, just pick any {U_i} it lies in to determine where it lands in {Z}. The map on sheaves can be defined similarly. \Box

So far we have managed to state an elementary and rather uninteresting exercise into categorical language. It is, however, a much more interesting theorem that representable functors are sheaves in significantly finer topologies.