I fell a bit behind on the continuation of the class field theory series because I was setting up a new laptop. Before I resume that, I want to talk about something very weird that I learned today.
Let be a set that omits at least two points. If
holomorphic and is such that
at one
, then
is the identity.
This is a striking rigidity phenomenon!
But how do we prove it? The idea is to consider the sequence of iterates . Suppose for simplicity
. Then in a neighborhood of
, we can write
, where the
are omitted higher terms. If
is not identically the identity, then
.
So, similarly, by direct computation, in some neighborhood of , we have
. Similarly, if we define
for notational convenience, we have
But the are all holomorphic maps into
. Since
omits at least two points, the family
is normal by Montel’s theorem and consequently has a subsequence
that converges uniformly on compact sets.
Thus the derivatives converge, which is impossible unless
.
Huh? I didn’t exactly see that coming. If is the unit disk, then at least it looks familiar. A holomorphic map
of the unit disk into itself sending zero to zero must satisfy
, and if equality holds
is a rotation. So perhaps this result should be thought of as a generalization of Schwarz’s lemma? (Nevertheless, the use of Montel’s theorem is quite a sledgehammer to prove something as elementary as Schwarz.)
I should say where I got this from: Krant’z Complex Analysis: The Geometric Viewpoint. Krantz didn’t prove exactly this, but the argument is the same. Either this is standard fare that I missed when learning basic complex analysis, or I’m turning Climbing Mount Bourbaki into a comedy routine.
May 25, 2010 at 8:31 pm
I’d think of this as maybe part of “fixed point theory” (which I know nothing about). If I recall, there are attracting fixed points and repelling fixed points. The key thing here is that since it is neither of those and is in some sense stable. Thus it must be some sort of rotation about the point (i.e. rigid), but you’ve required the derivative to be literally 1, so it is the identity.
it is neither of those and is in some sense stable. Thus it must be some sort of rotation about the point (i.e. rigid), but you’ve required the derivative to be literally 1, so it is the identity.
I know I didn’t prove anything. These are just the words that pop into my mind when I read the above. So I’m not sure how to get around Montel, but it seems that some textbook that deals with fixed point theory might have a way to do it.
May 26, 2010 at 2:38 pm
It’s funny, because Krantz actually has another fixed point theorem (of Farkas and Ritt) in his book. It goes as follows: suppose is a holomorphic map of hte unit disk whose image has closure contained in
is a holomorphic map of hte unit disk whose image has closure contained in  .
.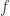 has a unique fixed point (existence is of course immediate from Brouwer).
has a unique fixed point (existence is of course immediate from Brouwer). with the Poincare metric (in which
with the Poincare metric (in which  is complete), since Schwarz’s lemma implies that
is complete), since Schwarz’s lemma implies that 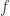 is a contraction.
is a contraction.
Then
The proof is actually an application of the classical Banach fixed point theorem, applied to
It must really be a rigidity statement, because it isn’t just topological: the hypothesis of holomorphicity is key. Incidentally, if we only assume that has modulus 1, then
has modulus 1, then 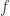 is still a bijective conformal map of
is still a bijective conformal map of 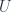 onto itself – this is the theorem in Krantz out of whose proof I extracted the post.
onto itself – this is the theorem in Krantz out of whose proof I extracted the post.