Representations of semidirect products

So, the blog stats show that semisimple Lie algebras haven’t exactly been popular. Traffic has actually been unusually high, but people have been reading about the heat equation or Ricci curvature rather than Verma modules. Which is interesting, since I thought there was a dearth of analysts in the mathosphere. At MathOverflow, for instance, there have been a few complaints that everyone there is an algebraic geometer. Anyway, there wasn’t going to be that much more I would say about semisimple Lie algebras in the near future, so for the next few weeks I plan random and totally disconnected posts at varying levels (but loosely related to algebra or algebraic geometry, in general).

I learned a while back that there is a classification of the simple modules over the semidirect product between a group and an commutative algebra which works the same way as the (more specific case) between a group and an abelian group. The result for abelian groups rather than commutative rings appears in a lot of places, e.g. Serre’s Linear Representations of Finite Groups or Pavel Etingof’s notes. I couldn’t find a source for the more general result though. I wanted to work that out here, though I got a bit confused near the end, at which point I’ll toss out a bleg.

Let ${G}$ be a finite group acting on a finite-dimensional commutative algebra ${A}$ over an algebraically closed field ${k}$ of characteristic prime to the order of ${G}$ . Then, the irreducible representations of ${A}$ correspond to maximal ideals in ${A}$ , or equivalently (by Hilbert’s Nullstellensatz!) homomorphisms ${\chi: A \rightarrow k}$ , called characters. In other words, ${A}$ acts on a 1-dimensional space via the character ${\chi}$ .

It is of interest to determine the irreducible representations of the semidirect product ${G \rtimes A}$ . This algebra is finite dimensional. So, all simple representations are finite-dimensional. Fix one, say ${V}$ . Then ${V}$ contains a simple ${A}$ -representation, i.e. there is a character ${\chi}$ and a vector ${v \in V}$ such that

$\displaystyle av = \chi(a) v , \quad \forall a \in A.$

Now consider the ${G}$ -representation ${k[G] v \subset V}$ . It is in fact ${A}$ -stable, because

$\displaystyle a (gv) = g (g^{-1} a g) v = g \chi(a^{g^{-1}}) v .$

Here ${a^{g^{-1}}}$ , of course, denotes ${g^{-1}}$ acting on ${a}$ .

Let ${G_\chi \subset G}$ be the set of elements of ${G}$ that fix the character ${\chi}$ . Then the above calculation shows that ${G_\chi}$ fixes the “weight space” of ${\chi}$ with respect to ${A}$ . In other words, if ${v}$ satisfies the above condition (that ${av = \chi(a)v, \forall \ a\in A}$ ) then so does ${g v}$ for ${g \in G_{\chi}}$ . In particular, ${k[G_\chi]v \subset V}$ is a ${G_\chi}$ -submodule on which ${A}$ acts by scalar multiplication by ${\chi}$ . Let ${V' \subset k[G_\chi]v}$ be an irreducible ${G_\chi}$ -representation.

Now there is a map of ${G_\chi \rtimes A}$ -representations, ${V' \rightarrow V}$ , so by Frobenius reciprocity, we get a map

$\displaystyle k[G \rtimes A] \otimes_{k[G_\chi \rtimes A ]} V' \rightarrow V.$

It is surjective, since the image is nonzero and ${V}$ is irreducible. I claim in fact that it is injective. For this, it is sufficient to check that if ${g, g' \in G}$ are in different ${G_\chi}$ right-cosets, then ${ gV' \cap g' V' = \{ 0 \}}$ . [Edit: This is not quite the case, cf. Darij’s comment below. -AM, 3/2/2010] This follows because an element in the intersection of the two is a weight for the characters ${\chi_1 = (\chi)^{g^{-1}}, \chi_2=(\chi)^{g'^{-1}}}$ , and ${g^{-1}, g'^{-1}}$ do not lie in the same left coset modulo ${G_\chi}$ .

We have obtained most of:

Theorem 1

An irreducible representation of ${G \rtimes A}$ can be obtained as follows. Fix a character ${\chi : A \rightarrow k}$ , the stabilizer ${G_\chi \subset G}$ , an irreducible ${G_\chi}$ -representation ${V'}$ which we let ${A}$ act on via ${\chi}$ , and set $\displaystyle V = \mathrm{Ind}_{G_\chi \rtimes A}^{G \rtimes A} (V').$

These exhaust the irreducible representations of ${G}$ .

What remains to be seen is that any ${V}$ as defined above by such an induction process is indeed irreducible. This may be proved as follows. ${V}$ can be written as a direct sum

$\displaystyle V = \bigoplus_{\lambda} V_{\lambda}$

where ${A}$ acts by ${\lambda}$ on ${V_{\lambda}}$ . (Shades of the weight space decomposition.) Here ${\lambda}$ ranges over the characters in the orbits of ${\chi}$ . Let they be enumerated as ${\lambda_1, \dots, \lambda_n}$ . I claim now that there is ${a \in A}$ such that ${\lambda_i(a) \neq \lambda_j(a)}$ for ${i \neq j}$ ; this follows from the Chinese remainder theorem applied to the maximal ideals associated with the ${\lambda_i}$ .

Anyway, choose some ${v \in V}$ , which we write as ${v_1 + \dots + v_n}$ for ${v_i \in V_{\lambda_i}}$ . We will prove that ${(G \rtimes A) v = V}$ .

Since ${G}$ permutes the ${V_{\lambda}}$ transitively, we find that ${k[G] v}$ itself contains a vector all of whose components in the ${V_{\lambda_i}}$ are nonzero. So, replacing ${v}$ by this vector, we may assume each ${v_i \neq 0}$ .

Then, if we multiply by ${a}$ (which was chosen as above), we have ${a^k v \in (G \rtimes A) v}$ for all ${k}$ . In particular,

$\displaystyle \lambda_1(a)^k v_1 + \dots + \lambda_n(a)^k v_n \in (G \rtimes A) v$

for all ${k}$ . If we invert since the vanderMonde determinant is nonzero, we find each ${v_i \in (G \rtimes A) v}$ . Since ${V_{\chi}}$ is ${G_\chi}$ -irreducible and generates ${V}$ , this implies that ${v}$ generates ${V}$ .

It is clear that changing the orbit of ${\chi}$ does not affect the module ${V}$ constructed above (up to isomorphism).

We have a uniqueness result as well:

Theorem 2 The representations ${V_{\chi_1}, V_{\chi_2}}$ associated to ${\chi_1, V'}$ and ${\chi_2, V'_2}$ are nonisomorphic when ${\chi_1, \chi_2}$ lie in different orbits of ${G}$ or if they are equal but ${V' \simeq V'_2}$ .

The eigenvalues of the action of ${a \in A}$ on ${V_{\chi_1}}$ (resp. ${V_{\chi_2}}$ ) are given by ${\lambda(a)}$ for ${\lambda}$ in the orbit of ${\chi_1}$ (resp. ${\chi_2}$ ), which proves that ${V_{\chi_1} \not\simeq V_{\chi_2}}$ unless ${\chi_1, \chi_2}$ are in the same orbit.

Now if ${\chi_1 = \chi_2}$ but ${V' \not\simeq V'_2}$ , we must show that ${V_{\chi_1} \not \simeq V_{\chi_2}}$ . I’m getting stuck here—does anyone know what to do? [Edit- Answered in comments.]

darij Says:

March 2, 2010 at 8:38 pm

“I claim in fact that it is injective. For this, it is sufficient to check that if ${g, g’ \in G}$ are in different ${G_\chi}$ right-cosets, then ${ gV’ \cap g’ V’ = \{ 0 \}}$”

I don’t think this is sufficient. The element that gets mapped to zero may be the sum of more than two pure tensors… However, this is easily fixed (you just need to invoke the linear independence of characters).

As for the remainder of the proof, it seems to me that the proof of Theorem 4.75 (i) and (ii) in Etingof’s notes does extend to your generalization, and (iii) has been done by you. But it’s 3 AM here, so I may be mistaken quite easily.

Akhil Mathew Says:

March 2, 2010 at 8:54 pm
Thanks for the correction on injectivity. Also, I think you’re right that the proof of (ii) in Etingof’s notes does extend (you choose an irreducible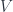 $V$ and pick an eigenvector of 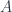$A$ ; this yields some character, which is uniquely determined up to the orbit of 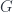$G$ . So there is a reverse correspondence from irreducibles to orbits of characters). The part that doesn’t has to do with the dimension count, because 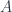$A$ isn’t a group, but I have already done the proof that these form a complete set.

1. darij Says:
  
  March 3, 2010 at 5:56 am
  Actually, even the dimension count can be saved if you really want to save it. You can show that
  
  sum_{U,O} dim V_{(U,O)}^2 = |G| |A^dual|
  
  like Etingof did. Now, |G| |A^dual| isn’t exactly the same as |G sem A| (where sem means semidirect product; sorry, I don’t have the slightest idea how to write LaTeX on wordpress blogs), but it will already be enough to show that
  
  |G| |A^dual| >= dim ((G sem A) / Rad (G sem A)).
  
  Now, |A^dual| = dim (A / Rad A) = dim A – dim Rad A and dim ((G sem A) / Rad (G sem A)) = dim (G sem A) – dim (Rad (G sem A)) = |G| dim A – dim (Rad (G sem A)), and thus we must prove that
  
  |G| (dim A – dim Rad A) >= |G| dim A – dim (Rad (G sem A)).
  
  This rewrites as
  
  |G| dim Rad A <= dim (Rad (G sem A)).
  
  This will follow once we have shown that G sem (Rad A) lies in Rad (G sem A). In order to show this, notice that Rad A is a nilpotent ideal of A (since the Jacobson radical of A is the nilradical of A), and thus G sem (Rad A) is a nilpotent ideal of G sem A (by an easy computation, since the action of G keeps Rad A among itself).
  
2. Akhil Mathew Says:
  
  March 3, 2010 at 9:43 pm
  Sorry, I really can’t respond to this now. I’ll get back to you.
  
3. Akhil Mathew Says:
  
  March 6, 2010 at 6:53 am
  Hold on–isn’t $A^{\vee}$ generally going to be infinite?