A theorem of Mazur-Ulam on isometries of vector spaces

Today’s will be a relatively short post, and primarily algebraic. I had mentioned a couple of days back the following result:

Theorem 1 (Mazur-Ulam) An isometry ${M: X \rightarrow X'}$ of a normed linear space ${X}$ onto another normed linear space ${X'}$ with ${M(0)=0}$ is linear.

We needed the theorem to show that a distance-preserving map between Riemannian manifolds is an isometry. Recall that $M$ ‘s being an isometry means that it preserves distances between points.

Apparently the theorem has no relation to Barry Mazur, but to another Mazur.

I will follow Lax’s Functional Analysis in the proof.

Reduction

It is enough to prove that

$\displaystyle M\left( \frac{x+y}{2}\right) = \frac{1}{2}(M(x) + M(y))\ \ \ \ \ (1)$

for all ${x,y \in X}$ .

Indeed, if this is the case, then by ${M(0)=0}$ , we get ${M\left( \frac{1}{2^n} x\right) = \frac{1}{2^n} M(x)}$ by induction. So

$\displaystyle M\left( \frac{k}{2^n} x\right) = \frac{k}{2^n} M(x)$

for all ${k}$ . By density of the dyadic fractions and continuity, we find ${M(kx)=kM(x)}$ for all ${k \in \mathbb{R}^+}$ . Also (1) and what’s already proved imply ${M(x+y) = M(x)+M(y)}$ , so ${M(-x)=-M(x)}$ , which proves linearity.

Strategy of the proof

The idea is to use a purely norm-theoretic way of describing the midpoint of ${x,y}$ . This must be reflected by ${M}$ , so it will prove (1). In particular, given ${x,y \in X}$ , we will define sets ${A_0, A_1, \dots}$ with ${\bigcap A_i = \{ \frac{1}{2}(x+y)\}}$ , with the sets defined solely in terms of the norm structure on ${X}$ . It will thus follow that ${M}$ maps these sets onto their analogs on ${X'}$ —which will prove (1) and the theorem.

${A_0}$

Henceforth, fix ${x,y \in X}$ . We define ${A_0}$ to be the set of points in ${X}$ which are midway between ${x,y}$ ; this means that ${w \in A_0}$ iff

$\displaystyle |w-y| = |w-x| = \frac{1}{2} |x-y|.$

Evidently the midpoint ${z}$ is in ${A_0}$ .

${A_1}$

Now ${A_0}$ is symmetric with respect to ${z}$ : ${2z - A_0 = A_0}$ . This is easily checked, as follows: if ${w \in A_0}$ , then

$\displaystyle |(2z-w)-y| = |x-w| = \frac{1}{2}|x-y|, etc.$

Also ${A_0}$ is bounded, ${d_0:=\mathrm{diam}(A_0) <\infty}$ . Then we can consider the set of points ${w' \in A_0}$ whose distance from any other point of ${A_0}$ is at most ${\frac{d}{2}}$ . An example is ${z}$ — ${A_0}$ is symmetric w.r.t. ${z}$ . We can repeat this inductively; see below.

${A_n}$

With this we need a general lemma:

Lemma 2 Let ${A \subset X}$ be a bounded set symmetric with respect to ${z}$ , with diameter ${d}$ . Then the set ${A'}$ of points ${w \in A}$ such that for ${w' \in A}$ arbitrary, ${|w-w'| \leq \frac{d}{2}}$ , satisfies the following properties:

${\mathrm{diam}(A') \leq \frac{\mathrm{diam}(A)}{2}}$ .

${z \in A'}$ .

${A'}$ is symmetric with respect to ${z}$ .

1 is easily checked from the definition of ${A'}$ . 2 follows from symmetry: if ${w' \in A}$ , then

$\displaystyle 2|z - w'| = |2z - 2w'| = |(2z - w') - w'| \leq d.$

For 3, suppose ${w \in A', w \in A}$ ; then

$\displaystyle | (2z - w') - w| = |(2z-w) - w'| \leq \frac{d}{2}$

since ${2z-w \in A}$ .

So we have defined with this notation ${A_1 = (A_0)'}$ , and inductively set ${A_n := (A_{n-1})'}$ ; each contains ${z}$ and is symmetric with respect to it. 1 in the lemma implies that ${\bigcap A_i = \{z\}}$ , so we’ve completed the proof by the strategy discussion. Indeed, it is clear from the description that ${M}$ maps ${A_i}$ bijectively to the corresponding sets ${B_i}$ between ${M(x),M(y)}$ .

A theorem of Mazur-Ulam on isometric maps of vector spaces « Delta Epsilons Says:

November 22, 2009 at 1:18 pm

[…] functional analysis. Tags: isometries, linear maps trackback I first posted this entry at Climbing Mount Bourbaki, where I have continued the MaBloWriMo series into topics in Riemannian geometry such as the […]

Todd Trimble Says:

November 11, 2011 at 10:56 am

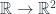Nice post! Just a couple of didactic remarks: it is crucial that $M$ be surjective for this proof to work, because one can cook up non-surjective isometries which are not affine. For instance, the map $\mathbb{R} \to \mathbb{R}^2$ defined by 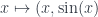$x \mapsto (x, \sin(x)$ is an isometry if $\mathbb{R}^2$ is equipped with the max (or $l_\infty$ ) norm. Also, the proof simplifies greatly if the codomain is strictly convex (no sphere contains a line segment), because already 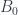$B_0$ consists of a single point. In this case, surjectivity is not even needed! 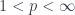As an example, the $l_p$ spaces for $1 < p < \infty$ are strictly convex.

Akhil Mathew Says:

November 11, 2011 at 6:38 pm
Thanks! These are interesting comments; I haven’t thought about this material in a while, and may use this in my section for the analysis class I’m TAing.

November 11, 2011 at 11:02 am

Also — you probably know this, but since you brought it up — the Mazur of this post is this guy. I’ll bet he and Ulam thought up this proof during a session at the Scottish Café in Lwow, in between bouts of drinking strong coffee and brandy.

Climbing Mount Bourbaki