The following topic came up in the context of my project, which has been expanding to include new areas of mathematics that I did not initially anticipate. Consequently, I have had to learn about several new areas of mathematics; this is, of course, a common experience at RSI. For me, the representation theory of Lie algebras has been one of those areas, and I will post here about it to help myself understand it. Right here, I’ll aim to cover the groundwork necessary to get to the actual representation theory in a future post.
Lie Algebras
Throughout, we work over , or even an algebraically closed field of characteristic zero.
Definition 1 A Lie algebra is a finite-dimensional vector space
with a Lie bracket
satisfying:
- The bracket
is
-bilinear in both variables.
for any
.
. This is the Jacobi identity.
To elucidate the meaning of the conditions, let’s look at a few examples.
Here are two easy ones:
Example 1 Any vector space is a Lie algebra with the bracket the zero map. Such Lie algebras are called commutative.
Example 2 Suppose
are Lie algebras. Then
is a Lie algebra as well, if the Lie bracket is defined as:
This is the direct sum
Lie algebras arise frequently in a more interesting way:
Definition 2 Let
be a finite-dimensional associative
-algebra. Then the Lie bracket of
is defined as
; this makes
into a Lie algebra, as is easily checked (but associativity is important).
Note in particular the resemblance of the Lie bracket to commutators in group theory. For instance, iff
commute with each other.
Many of the important Lie algebras in fact arise in this way, from rings, especially matrix rings:
Definition 3 Fix
. We define
as the Lie algebra coming as above from the ring of
-by-
complex-valued matrices, with the usual Lie bracket.
It is often of interest to consider Lie subalgebras of . One of the most important is
:
Definition 4
is the space of complex
-by-
matrices whose trace is zero.
One must actually check that is indeed a Lie subalgebra. But this follows from the identity
if are
-by-
matrices. So
, for any
.
Representations
In general, a representation of some algebraic object is an action of that object on a vector space in a manner compatible with its algebraic structure. In our case, this will mean respecting the bracket.
Definition 5 A representation of
is a
-linear map
(
is the space of
-by-
matrices, which is an associative algebra) such that
In other words it is a Lie algebra-homomorphism . This resembles the notion of group representations, where we had group-homomorphisms
.
One can also phrase the above definition in the following way.
Example 3 A (finite-dimensional) representation of
is a finite-dimensional vector space
with a
-bilinear map
, say denoted by
, such that
The equivalence of this phrasing with the previous one follows from the correspondence between linear transformations and matrices. Looking at the (initial) definition, a representation of on
means a map
if
has dimension
. Then, we define for
,
this gives a map , and since
is a Lie homomorphism, (2) is satisfied. Similarly, one can work the other way.
There is a parallel here with the notion of modules and even group representations, which arise if one takes an “enveloping algebra” of ; this, however, is better saved for a later post with more generality.
So, I’m planning to continue this series with a post on and its irreducible representations, and then possibly talk about Engel and Lie, semisimple Lie algebras, and further into representation theory.
July 16, 2009 at 10:39 pm
In definition 1, you have , and I believe you just mean L.
, and I believe you just mean L.
Here is a question I should probably know the answer to, and I feel sort of dumb for asking, but…every Lie group generates a Lie algebra. Is there some sort of relationship between the representation theory of G and say, the Lie group generated by G? My guess is that you lose information, since non-isomorphic Lie groups can generate the same Lie algebra (if my memory serves me correctly…). I haven’t gotten to the point in the summer where I review this for my qualifying exams, yet. So this is a nice jump start.
the Lie group generated by G? My guess is that you lose information, since non-isomorphic Lie groups can generate the same Lie algebra (if my memory serves me correctly…). I haven’t gotten to the point in the summer where I review this for my qualifying exams, yet. So this is a nice jump start.
July 16, 2009 at 11:51 pm
Thanks for the correction! I was initially intending to write something up on just , because it’s more relevant to my project to understand the representation theory, but then realized it made more sense to do the general case, and tried to fix an older version of the post.
, because it’s more relevant to my project to understand the representation theory, but then realized it made more sense to do the general case, and tried to fix an older version of the post.  will likely be the next post I write.
will likely be the next post I write.
As for your question: my understanding here is weaker than I would like, which is partially why I am writing these posts, but given a representation of a Lie group G, then one gets a representation of its Lie algebra, by taking differentials at the identity. One example of how to lose information could be a Lie group with infinitely many components, which has the same Lie algebra as one of the components. One might also lose information between covering spaces of Lie groups.
Still, given a representation of the Lie algebra of the simply connected Lie group G, i.e. a Lie-homomorphism , one gets a Lie group-homomorphism
, one gets a Lie group-homomorphism  by the “second principle” that Fulton and Harris refer to; as far as I know, this is just an application of the exponential map, and the universality of the Campbell-Hausdorff formula. Thus we should indeed get a bijection between representations of a simply connected Lie group and its Lie algebra. This is actually an idea for a future post, probably after July though.
by the “second principle” that Fulton and Harris refer to; as far as I know, this is just an application of the exponential map, and the universality of the Campbell-Hausdorff formula. Thus we should indeed get a bijection between representations of a simply connected Lie group and its Lie algebra. This is actually an idea for a future post, probably after July though.
July 17, 2009 at 12:34 am
Ah, right. If I wasn’t so lazy, that probably would have been one of the first things I encountered when looking for theorems of the sort I was referring to. I did learn that at one point, but forgot it.
July 17, 2009 at 5:25 am
This is an area I know nothing about, so I’m wondering what the functorial picture is for Lie algebra representations. For group representations and actions it’s clear: treating a group as a one-object category, a representation of
as a one-object category, a representation of  is just a functor into
is just a functor into  and a group action of
and a group action of  is just a functor into
is just a functor into  . Presumably one can also talk about representations of algebras in this way by enriching everything appropriately.
. Presumably one can also talk about representations of algebras in this way by enriching everything appropriately.
So what’s the functorial picture for Lie algebras? In other words, why is the commutator “universal” for Lie algebras? (This probably has a well-known explanation, but I’ve never seen it. Etingof’s notes on the subject introduce the definition of the universal enveloping algebra with no motivation at all.)
My best guess is that the process of finding the Lie algebra of a Lie group is also functorial and that all this should come out of the corresponding abstract nonsense, but again, I’d really appreciate someone clearing this up for me.
July 17, 2009 at 1:03 pm
Thanks for the comment!
Are you talking about a “categorification” of Lie algebra representations? satisfying some compatibility conditions), although I will need to think about it. I can ask my mentor about it today (it’s fairly relevant to my project anyway).
satisfying some compatibility conditions), although I will need to think about it. I can ask my mentor about it today (it’s fairly relevant to my project anyway).
First, I intend sometime to talk about enveloping algebras, which will play the analog of the group ring, and which I will try to motivate with some abstract nonsense at least. I would suspect that there may indeed be a categorification of this notion, at least for specific Lie algebras, in suitable tensor categories (e.g. if L is the algebra and M the object, there should be a map
“My best guess is that the process of finding the Lie algebra of a Lie group is also functorial”
This is true because any morphism of Lie groups induces a map on the tangent spaces at the identity. Since this is a homomorphism, it commutes with the adjoint action and thus with the Lie bracket.
July 17, 2009 at 4:47 pm
I brought this up today morning, and apparently yes, the notion of Lie algebra can be categorified to some extent at least.
Let’s say we are in an additive tensor category. We can say is a Lie algebra if there is a morphism
is a Lie algebra if there is a morphism  such that the morphism $L \otimes L \otimes L \to L$ coming from commutators satisfies some compatibility condition (i.e. should factor through the alternating product, and satisfy some analog of the Jacobi identity). Then we can define a representation of
such that the morphism $L \otimes L \otimes L \to L$ coming from commutators satisfies some compatibility condition (i.e. should factor through the alternating product, and satisfy some analog of the Jacobi identity). Then we can define a representation of  to be an object
to be an object  of the category with a morphism
of the category with a morphism  satisfying some compatibility conditions, etc. I think this can probably become a full post at some point (when I talk about my project, which is related to this kind of “categorification”* anyway).
satisfying some compatibility conditions, etc. I think this can probably become a full post at some point (when I talk about my project, which is related to this kind of “categorification”* anyway).
Does this answer your question?
*Strictly speaking, this may be the wrong word.
July 17, 2009 at 8:01 pm
Partially, but maybe what I’m looking for is a lifting of a Lie group representation to a Lie algebra representation that makes it obvious why the commutator is the “right” choice of bracket on .
.
July 17, 2009 at 8:13 pm
Well, I think the action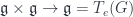 is derived as follows: take the map
is derived as follows: take the map 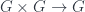 given by
given by  , differentiate with respect to
, differentiate with respect to  to get a map
to get a map  , then with respect to
, then with respect to  to get a map
to get a map  . I believe the fact that this gives the usual bracket on
. I believe the fact that this gives the usual bracket on  follows from a computation; I’m somewhat fuzzy on the details right now, as I haven’t really thought about Lie groups for a while now. I’ll probably post more about Lie groups later.
follows from a computation; I’m somewhat fuzzy on the details right now, as I haven’t really thought about Lie groups for a while now. I’ll probably post more about Lie groups later.
July 17, 2009 at 8:43 pm
[…] representation theory, semisimplicity, sl2 trackback is a special Lie algebra, mentioned in my previous post briefly. It is the set of 2-by-2 matrices over of trace zero, with the Lie bracket defined […]
July 18, 2009 at 1:28 pm
I think that no matter what, there has to be a “weird” step. I have a proof that![(Ad_* X)Y=[X, Y]](https://s0.wp.com/latex.php?latex=%28Ad_%2A+X%29Y%3D%5BX%2C+Y%5D&bg=ffffff&fg=29303b&s=0&c=20201002) by just computing at
by just computing at  (which seems to be your method). It turns out that
(which seems to be your method). It turns out that  .
.
So now the intuition gets weird unless you are really good with the geometric intuition of flows, since that is precisely the definition of the Lie derivative of with respect to
with respect to  at e, which is the Lie bracket at e. (It is still rather strange intuitively that the Lie derivative of vector fields is the Lie bracket).
at e, which is the Lie bracket at e. (It is still rather strange intuitively that the Lie derivative of vector fields is the Lie bracket).
July 18, 2009 at 1:42 pm
I believe this can be done directly: Let’s first fix the initial argument , and take the derivative of
, and take the derivative of 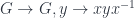 , in the setting where
, in the setting where  . We can let
. We can let 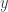 trace out the path
trace out the path 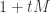 for some matrix
for some matrix  , which is the tangent vector as
, which is the tangent vector as 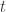 traces out some interval (and then take difference quotients, let
traces out some interval (and then take difference quotients, let  ). The derivative must thus send
). The derivative must thus send  . Now we can differentiate w.r.t
. Now we can differentiate w.r.t  in the direction
in the direction 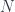 , say
, say 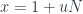 , i.e.
, i.e.  , and we apply the product rule: this is
, and we apply the product rule: this is  . We have to take as a lemma the derivative of
. We have to take as a lemma the derivative of 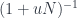 at
at  , but this can be checked using e.g. the geometric series.
, but this can be checked using e.g. the geometric series.
I don’t think we need the geometric intuition of flows here. Though alternatively, we could use the definition of the Lie bracket via left-invariant vector fields, but that would require a separate proof, which I should probably write up at some point to force myself to learn it properly.
July 18, 2009 at 3:06 pm
[…] The proof in our case runs as follows. Suppose . We must show , which is what the first assertion states. Indeed, by the definition of representations: […]
July 20, 2009 at 9:34 pm
[…] I’m going to get back eventually to the story about finite-dimensional modules, but for now, Lie algebras are more immediate to my project, so I’ll talk about them […]