Today, I want to talk a bit about group representation theory. Many of us (such as myself) are interested in representation theory in general and will likely talk more about it in the future, so it will be useful to summarize the essential ideas here to refer back. But the basics are well known and have been discussed at length on other blogs (see, e.g. here, which is discussing the subject right now), so I am merely going to summarize these facts without proofs. The interested reader can read these notes for full details. Then, I’ll mention a property to be used later on.
What is a group representation?
Start with a group . At least for now, we’re essentially going to be constructed with finite groups, but many of these constructions generalize. A representation of
is essentially an action of
on a finite-dimensional complex vector space
.
Formally, we write:
Definition 1 A representation of the group
is a finite-dimensional complex vector space
and a group-homomorphism
. In other words, it is a group homomorphism
, where
, and
is the group of invertible
-by-
matrices.
An easy example is just the unit representation, sending each to the identity matrix.
Alternatively, we can form the group ring of
; this consists of formal sums
for coefficients
. It is made into a ring by pointwise multiplication: we demand that multiplication in the group ring match multiplication in the group, and be linear.
Phrased in this language, a representation of is just a
-module.
Maschke’s Theorem
One of the nice facts about group representation theory is that we can split a representation of a group into “atoms” which contain no smaller elements. Formally, we write:
Definition 2 A nonzero representation
of the group
is said to be simple or irreducible if
(which is a
module) contains no proper
-modules other than zero.
The following is Maschke’s theorem, which we state without proof:
Theorem 3 A representation
of
can be written as a direct sum,
where the
‘s are simple representations, and the
are integers.
The decomposition is also unique up to isomorphism. (Note that the direct sum of representations is a representation itself.)
This is equivalent to saying that the group ring is semisimple.
[Edit, 6/14- for a proof of Maschke’s theorem, see this post, which appeared after this one..]
The Regular Representation
Any ring is automatically a (left)
-module. In particular, the group ring
is itself a
-module, which is also a finite-dimensional vector space, if
is a finite group.
Thus the underlying vector space of
is a representation of
. This is called the regular representation.
The following is the fundamental property of the regular representation:
Theorem 4 When decomposed into simple components, the regular representation of a finite group
contains each simple component with multiplicity equal to the dimension of that component.
So, in particular, there are only finitely many such (non-isomorphic) simple representations, a fact which can be proved more generally for semisimple algebras.
Characters and Class Functions
Given a representation for a vector space, we define the corresponding function
by
.
Definition 5
is called the character of
.
From the basic properties of traces, characters are additive on direct sums, i.e. . Moreover, characters are multiplicative on tensor products.
From the properties of traces (specifically for matrices
), we see that the characters
are class functions; that is,
for all
. The characters are invariant under inner automorphisms.
Theorem 6 The irreducible characters of
form a basis of the vector space of class functions on
.
In particular, this implies the number of irreducible representations of , up to isomorphism, is given by the number of conjugacy classes.
This basis is actually orthonormal with respect to the Hermitian inner product on the space of class functions defined as follows:
because of the following:
Theorem 7 For irreducible representations
, we have
if
are isomorphic, and
otherwise.
In particular, putting Maschke’s theorem and this together, we see that to find the multiplicties with which an irreducible occurs in
, one just takes the inner product
.
I want to end this post with a random remark that will become useful later on.
First of all, our matrices for
defining a representation are actually diagonalizable. We know from linear algebra that we can put such a matrix in a triangular form, but we also know that some power of them is the identity:
. So fix
, a triangular matrix, which satisfies
for some
. I claim
is diagonal. Indeed, the condition means
, or
satisfies
. In particular, the minimal polynomial of
divides
. Since
has no repeated roots, the minimal polynomial also has none. By a general theorem of linear algebra, this implies
is diagonalizable. Moreover, let the diagonal entries be
. Then each
satisfies
.
In this case, the trace is just the sum
. It follows that the character
is always a sum of
-th roots of unity and is in particular an algebraic integer.
This fact will be useful to us later, as we talk about applications of group representation theory. It will also enable us to show that the dimensions of group representations divide the group order. For now though, I’ll leave it here.
July 12, 2009 at 3:31 am
The Princeton Companion article on representation theory has an interesting snippet about why representation theory works out so much more nicely than the theory of group actions. Offhand, the two are superficially very similar: just as a representation is a homomorphism where the latter lies in the category of finite vector spaces, a group action is a homomorphism
where the latter lies in the category of finite vector spaces, a group action is a homomorphism 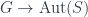 where the latter lies in the category of finite sets and bijections.
where the latter lies in the category of finite sets and bijections.
The problem, according to the article, is that understanding the “irreducible” (transitive) group actions requires understanding the entire subgroup lattice of a group, which can be exponentially larger than the group itself. However, the nice categorical properties of somehow force us to restrict our attention to conjugacy structure, with the result that there are as many irreducible representations as conjugacy classes. Of course there are fewer of these than group elements.
somehow force us to restrict our attention to conjugacy structure, with the result that there are as many irreducible representations as conjugacy classes. Of course there are fewer of these than group elements.
The issue appears to be that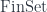 isn’t additive. Decomposing a given group action with respect to disjoint union is easy (they’re given by the orbits), but decomposing with respect to Cartesian product appears to be hard (at least I’ve never heard anyone talk about it), and in
isn’t additive. Decomposing a given group action with respect to disjoint union is easy (they’re given by the orbits), but decomposing with respect to Cartesian product appears to be hard (at least I’ve never heard anyone talk about it), and in  we get to do both at the same time.
we get to do both at the same time.
July 12, 2009 at 10:30 pm
Thanks for the comment! That is, indeed, an interesting observation, that the simple imposition of linearity conditions on a group action can drastically change the structure of irreducible objects. This also seems to relate to the reason characteristic zero (or more generally a characteristic prime to the group order) is necessary for the nice parts of character theory to work; in this case, the additive structure still exists, but averaging doesn’t work (just as it doesn’t for finite sets).
July 25, 2009 at 5:09 pm
[…] in algebra. Tags: enveloping algebras, Lie algebras, tensor algebras trackback As we saw in the first post, a representation of a finite group can be thought of simply as a module over a certain ring: the […]
August 30, 2009 at 3:44 pm
[…] has some posts about the basic results of group representation theory, and Akhil Mathew over at Delta Epsilons has also written about group representations. (For the sake of completeness, there are also the […]
September 20, 2009 at 10:57 am
[…] summarized the basic general facts about group representation theory here, which we we will need here. For more complete details, see the references there to other […]
September 23, 2009 at 5:15 pm
[…] to cover a quick and relevant lemma in group representation theory (referring as usual to the past blog post as […]
September 19, 2010 at 9:12 pm
I’m starting at the beginning of your blog. Looks great! I look forward to learning about algebra and algebraic *** at your feet … and at the foot of Mount Bourbaki.
September 19, 2010 at 9:13 pm
Qiaochu or Akhil, can you post a link to the Princeton Companion article mentioned in Qiaochu’s comment?
September 23, 2010 at 3:37 am
Don’t learn by just reading the blog – at least I wouldn’t recommend it. Pick a good book on the subject, learn from that book and then consult this blog for extra explanation. The reason is that while Akhil’s blog is excellent, and he should be commended for creating such a wonderful blog on mathematics, it often tends to deviate between topics quite frequently (as Akhil himself says, his interests change frequently). So unless you don’t mind learning representation theory in the morning, schemes in the afternoon and homotopy theory at midnight, all in one day, I’d recommend reading a book on something that this blog does a lot on (like algebraic geometry), and consulting the blog topics ON algebraic geometry as an additional source. Stick to one topic at a time and use the blog posts on that topic as an additional ref. Just my 2 cents BTW.
September 23, 2010 at 9:13 pm
Nah, I hate-hate-hate the yellow spiney book approach. I like learning eclectic ideas in a casual atmosphere.