The purpose of this post is to show that the category of finite-dimensional representations of a semismple Lie algebra is a semisimple category; there is thus an analogy with Maschke’s theorem, except in this case the proofs are more complicated. They can be simplified somewhat if one uses the cohomology of Lie algebras (i.e., appropriate Ext groups), which I may talk more about, but most likely only later. Here we will give the proofs based on linear algebra.
The first step is to construct certain central elements in the enveloping algebra.
Casimir elements
Let be a nondegenerate invariant bilinear form on the Lie algebra
. (E.g.
could be semisimple and
the Killing form.) Given a basis
, we can consider the dual basis
with respect to it, i.e. such that
. Consider the Casimir element
I claim that is independent of the choice of
and is in the center of the enveloping algebra. First off, consider the isomorphisms of
-modules,
The last one is given by the form .
Now the identity, an invariant element of , is sent to
. Since there is a well-defined homomorphism of vector spaces,
we see that is unique. Moreover, we can make
into a
-module by the adjoint—or, equivalently, commutator—mapping, i.e.
for
. Then
becomes a
-homomorphism, because
while
So is then an invariant element under this action of
on
, which means that
is in the center of
.
Complete reducibility
Lemma 1 Let
be a semisimple subalgebra. Let
be the bilinear form via
. Then
is nondegenerate on
.
Now is the form associated to the representation
so is invariant. The kernel of the form is thus an ideal
, and by the second version of Cartan’s solvability criterion,
is solvable. This proves the lemma. One half the proof of Cartan’s semisimplicity criterion can be generalized, as it shows.
Fix a semisimple Lie algebra over a field
of characteristic zero. Let
be a simple
-representation, i.e. containing no proper subrepresentations besides zero.
Lemma 2 (Raising of invariants) Consider an exact sequence of
-modules
where
is acted upon trivially. Then it splits.
We prove this by induction on . If
is not simple, then we can take a smaller submodule
and consider the sequence
We get by the inductive hypothesis a -section
, whose image is a one-dimensional submodule
. Then
.
There is another exact sequence
from which we can take a section , whose image
satisfies
. In particular,
.
So we may assume simple, and work with our exact sequence
as before.
We may make one further reduction, namely to assume that the action of on
is faithful. If
is the kernel of this action, it is an ideal—and, as a direct summand in
, semisimple itself (as a Lie algebra). I claim that this ideal acts trivially on
. Now,
sends
into
because it acts trivially on
. Since
, it follows that
must act trivially on
. So we can treat our sequence as a sequence of
-modules, where this quotient is a semisimple Lie algebra (as
was a direct factor).
We have now made the reduction of the previous lemma to the following claim:
Lemma 3 (Special case) Let
be a faithful, simple representation of the semisimple Lie algebra
and consider an exact sequence
this splits.
We have the nondegenerate bilinear form and the corresponding Casimir element
. Then
acts trivially on
; so
. Moreover, I claim
. Indeed,
is a
-endomorphism of
, and once we prove it is nonzero, it will follow that it is an isomorphism. But
since we are in characteristic zero.
As a result, we take a nonzero vector annihilated by
as the splitting. Then
, so
is invariant.
Finally, we can do the general case:
Theorem 4 (Weyl) Let
be a
-submodule of the finite-dimensional representation
of the semisimple Lie algebra
. Then
has a
-complement.
(I.e. the category is semisimple.)
We can assume that is simple (i.e. contains no proper subrepresentations). It then follows by induction that every finite-dimensional
-module is a semisimple module, which implies the theorem.
So, there is an exact sequence of -modules
We consider the submodule of
consisting of multiples of the identity and the inverse image
; this is then a
-submodule as well. There is an exact sequence
By the previous result on raising invariants, we can find a 1-dimensional -submodule of
which maps isomorphically onto
. Note that any 1-dimensional
-module is the trivial (action by zero) one because
. This 1-dimensional module is generated by some
-invariant
which restricts to a nonzero multiple of the identity on
. An appropriate multiple gives a
-invariant projection
and thus a complement.
This result is hugely important, as we will see in the future.
January 31, 2010 at 11:39 am
[…] Climbing Mount Bourbaki Thoughts on mathematics « Weyl’s theorem on complete reducibility […]
January 10, 2011 at 11:48 am
I’ve got some questions here, and a few typos. Otherwise, thanks for this nice review!
– Shortly before Lemma 1, the $axa$ in http://l.wordpress.com/latex.php?latex=%5Cdisplaystyle+f%28+%5Bx%2Ca%5D+%5Cotimes+b+%2B+a+%5Cotimes+%5Bx.b%5D%29+%3D+xab+-+axa+%2B+axb+-+abx.&bg=ffffff&fg=000000&s=0 should be $axb$, and the $[x.b]$ should be $[x,b]$ (though it’s maybe a problem with rendering precision).
– In Lemma 1, the $\to$ arrow should be $\mapsto$.
– First sentence after Lemma 1: “representation of $V$” should either be “representation on $V$” or “representation $V$”. $V$ is not an algebra.
– Proof of Lemma 2: “We may one further reduction, that the action of $\mathfrak g$ on $V$ is faithful.” This sentence needs two more words: “We may DO one further reduction, ASSUMING that the action of $\mathfrak g$ on $V$ is faithful.” or something like that.
– Shortly after that: “and, as a direct summand in $\mathfrak g$, semisimple itself”. “Semisimple” may mean “semisimple as $\mathfrak g$-module” or “semisimple as Lie algebra”. You mean the latter here, I think.
– Before you can redduce Lemma 2 to Lemma 3, you need to ensure that $\mathfrak g / \mathfrak n$ is semisimple. This is, of course, easy since $\mathfrak g / \mathfrak n = \mathfrak n^{\perp}$.
– Shortly before Theorem 4, you write $\mathfrak g v = C \mathfrak g v = \mathfrak g C v = 0$. The first equality sign should be an isomorphism sign, I think.
– The proof of Theorem 4 is obscure to me (but I know a different one from Weibel, so this is not important anyway). Why can we assume that $W$ is simple? (Here is where I would use the long exact sequence in Lie algebra cohomology…) Why is your exact sequence of $hom$’s exact? How do you know that the submodule $hom_{\mathfrak g} (W,W)$ consists of multiples of the identity? (This kind of Schur needs $k$ to be algebraically closed).
January 10, 2011 at 9:25 pm
Thanks for the corrections! I’ve made the changes (apparently I didn’t pay too much attention when writing this post — I think I was on some kind of blogging spree).
To be honest, I haven’t thought about this in a while and can’t remember the argument well, but I may have been assuming that the field was algebraically closed at the beginning. The restriction to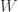 simple is reasonable because every object in this category is artinian, so contains a simple subobject; then keep splitting off chunks (so any object decomposes into a sum of simple ones since the category is artinian).
simple is reasonable because every object in this category is artinian, so contains a simple subobject; then keep splitting off chunks (so any object decomposes into a sum of simple ones since the category is artinian).
January 10, 2011 at 6:06 pm
I think I know how to prove Theorem 4 now. The idea comes from: C. A. Weibel, “An Introduction to Homological Algebra”, proof of Theorem 7.8.11. Weibel uses $H^1$ rsp. $\operatorname*{Ext}$ groups to do this proof, but this all can be rewritten in elementary terms:
Let $U = V / W$, so we have a short exact sequence $0 \to W \to V \to U \to 0$. Let $E$ be the subspace of $\operatorname*{hom}_k (W, W)$ generated by $\operatorname*{id}$, and let $F$ be the preimage of this subspace $E$ under the canonical map $\operatorname*{hom}_k (V, W) \to $\operatorname*{hom}_k (W, W)$ (which is induced by the inclusion map $W\to V$). Then, the image of the map $\operatorname*{hom}_k (U, W) \to \operatorname*{hom}_k (V, W)$ (which is induced by the epimorphism $V \to U$) is contained in $F$, and the sequence
$0 \to \operatorname*{hom}_k (U, W) \to F \to E \to 0$
is a short exact sequence of $\mathfrak g$-modules (this is easy to prove). Since $E\cong k$ as $\mathfrak g$-module (this is obvious), we can replace $E$ by $k$ in this sequence, and thus Lemma 2 yields that this sequence splits. Thus, the element $\operatorname*{id} \in E$ can be lifted by a $\mathfrak g$-module homomorphism $E \to F$ to an element of $F$. This element of $F$ will be $\mathfrak g$-invariant and thus a $\mathfrak g$-module homomorphism from $V$ to $W$. And being a lift of $\operatorname*{id}$, this homomorphism must be a section for the short exact sequence $0 \to W \to V \to U \to 0$. So this short exact sequence splits, i. e. the submodule $W$ of $V$ has a $\mathfrak g$-complement. Done.
January 10, 2011 at 9:28 pm
Right. OK, so I suspect this is kind of the same argument (it’s due to Weyl, I think? — there’s a nicer one if you allow Lie groups, because then the Lie algebra corresponds to a compact group and you can use the usual averaging trick as in Maschke’s theorem, with integration w.r.t. the Haar measure replacing averaging) but I am not really sure. I will get back to you after I actually flip through a book on Lie algebras so that I refresh my memory on this!